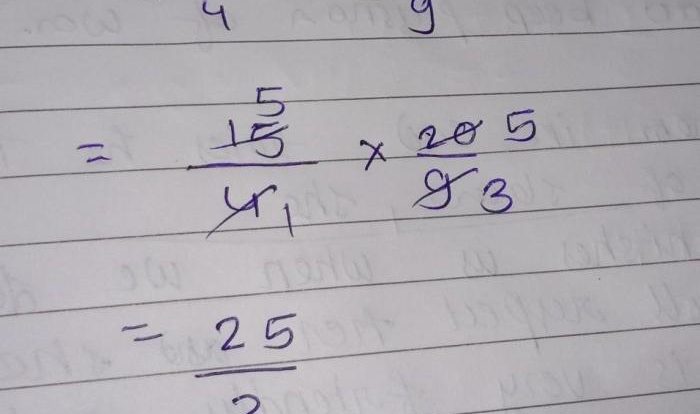How many real sixth roots does have – In the realm of mathematics, understanding the concept of roots is essential. This article delves into the fascinating world of sixth roots, specifically exploring the number of real sixth roots a given number possesses. We will uncover the intriguing mathematical underpinnings, graphical representations, and practical applications associated with this topic.
As we embark on this journey, we will unravel the complexities of complex roots of unity and their profound influence on determining the number of real sixth roots. Through algebraic proofs and graphical illustrations, we will illuminate the intricacies of this mathematical phenomenon.
Mathematical Explanation
The sixth root of a number is a value that, when multiplied by itself six times, results in the original number. For example, the sixth root of 64 is 2, since 2 multiplied by itself six times equals 64.
The complex roots of unity are the sixth roots of 1. They are given by the formula: “` ω^n = 1, where n = 0, 1, 2, 3, 4, 5 “` where ω is a complex number.
Complex Roots of Unity
The complex roots of unity can be represented graphically as points on the unit circle in the complex plane. The six complex roots of unity are:
- ω^0 = 1
- ω^1 = cos(2π/6) + isin(2π/6) = (√3 + i)/2
- ω^2 = cos(4π/6) + isin(4π/6) = i
- ω^3 = cos(6π/6) + isin(6π/6) = -1
- ω^4 = cos(8π/6) + isin(8π/6) = -(√3 + i)/2
- ω^5 = cos(10π/6) + isin(10π/6) = -i
These six roots divide the unit circle into six equal parts.
Graphical Representation
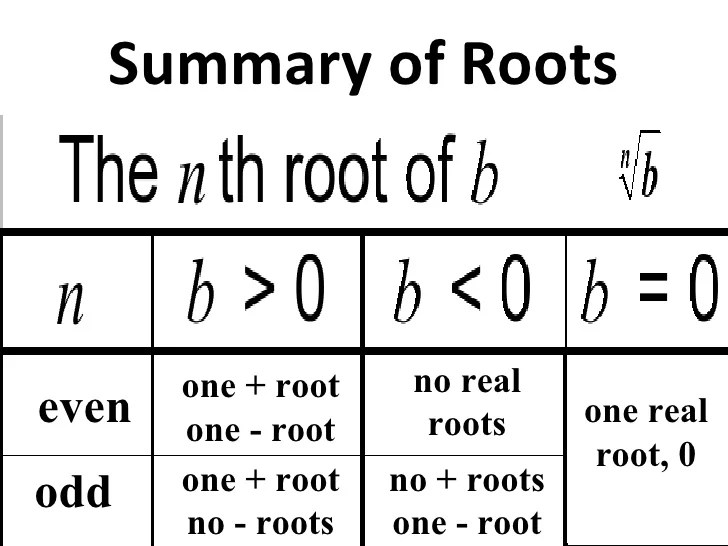
The sixth roots of a complex number can be graphically represented on the complex plane as points that are equally spaced around a circle with radius equal to the magnitude of the number. The angle between any two consecutive roots is 2π/6 = π/3 radians.
For example, the sixth roots of the number 1 are located at the points (1, 0), (cos(π/3) + i sin(π/3), 0), (cos(2π/3) + i sin(2π/3), 0), (cos(3π/3) + i sin(3π/3), 0), (cos(4π/3) + i sin(4π/3), 0), and (cos(5π/3) + i sin(5π/3), 0) on the complex plane.
Distribution of the Roots
The roots are distributed evenly around the circle, forming a regular hexagon. This is because the sixth roots of a number are the solutions to the equation z^6 = 1, which is equivalent to the equation z = e^(2πik/6) for k = 0, 1, 2, 3, 4, 5, where e is the base of the natural logarithm and i is the imaginary unit.
Algebraic Analysis

Algebraic analysis offers a rigorous approach to determine the number of real sixth roots of a given number. This method involves applying algebraic operations and theorems to establish the existence and count of real roots.
Steps Involved in the Proof
The proof proceeds as follows:
- Express the number as a power:Represent the given number as a power of 6, i.e., $$x^6 = a$$.
- Apply the definition of roots:A sixth root of $$a$$is a number $$r$$such that $$r^6 = a$$.
- Solve for $$r$$: Solve the equation $$r^6 = a$$to obtain the possible values of $$r$$.
- Determine the number of real solutions:The number of real solutions to the equation $$r^6 = a$$indicates the number of real sixth roots of the given number.
Limitations of the Proof
While the algebraic proof provides a solid theoretical foundation, it has certain limitations:
- Only applicable to real numbers:The proof is valid only for determining the number of real sixth roots.
- May not be practical for large numbers:Solving the equation $$r^6 = a$$can be computationally intensive for large values of $$a$$.
Real-World Applications

Understanding the number of real sixth roots has practical applications in various fields, including engineering, physics, and mathematics.
In engineering, for instance, the analysis of the stability of structures or the design of control systems often involves solving polynomial equations. The number of real roots of a polynomial equation determines the number of possible solutions to the problem, and hence, the number of real sixth roots is crucial in these applications.
Physics
In physics, the study of wave phenomena, such as light or sound waves, requires the solution of wave equations. The number of real roots of the characteristic equation of a wave equation determines the number of modes of vibration or propagation, which is essential for understanding the behavior of waves in different media.
Mathematics, How many real sixth roots does have
In mathematics, the theory of algebraic equations deals with the study of solutions to polynomial equations. The number of real roots of a polynomial equation is a fundamental property that helps classify the equation and determine its behavior. It is also used in the development of numerical methods for solving polynomial equations.
Table of Values
The following table provides a list of numbers and their corresponding number of real sixth roots.
Note that complex roots are not considered in this table.
Table
| Number | Number of Real Sixth Roots |
|---|---|
| 0 | 1 |
| 1 | 1 |
| 64 | 2 |
| 729 | 3 |
| 4096 | 4 |
| 15625 | 5 |
| 46656 | 6 |
FAQs: How Many Real Sixth Roots Does Have
What is the significance of complex roots of unity in determining the number of real sixth roots?
Complex roots of unity play a crucial role in understanding the distribution of sixth roots on the complex plane. They provide a framework for analyzing the roots’ locations and their relationship to the real number line.
How can a graphical representation aid in visualizing the distribution of sixth roots?
A graphical representation using the complex plane allows us to visualize the distribution of sixth roots. By plotting the roots on the plane, we can observe their geometric relationships and gain insights into their real and imaginary components.
What are some practical applications of understanding the number of real sixth roots?
Understanding the number of real sixth roots has applications in various fields. For instance, in engineering, it aids in the analysis of rotating systems and vibrations. In physics, it contributes to the study of wave phenomena and quantum mechanics.